Ley de Coulomb:
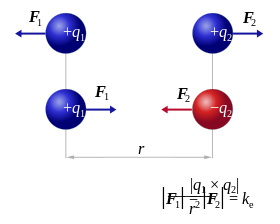
- La magnitud de cada una de las fuerzas eléctricas con que interactúan dos cargas puntuales en reposo es directamente proporcional al producto de la magnitud de ambas cargas e inversamente proporcional al cuadrado de la distancia que las separa.
Charles-Augustin de Coulombbalanza de torsión desarrolló la
con la que determinó las propiedades de la fuerza electrostática. Este
instrumento consiste en una barra que cuelga de una fibra capaz de
torcerse. Si la barra gira, la fibra tiende a hacerla regresar a su
posición original, con lo que conociendo la fuerza de torsión que la
fibra ejerce sobre la barra, se puede determinar la fuerza ejercida en
un punto de la barra. La ley de Coulomb también conocida como ley
de cargas tiene que ver con las cargas eléctricas de un material, es
decir, depende de si sus cargas son negativas o positivas.
En la barra de la balanza, Coulomb colocó una pequeña esfera cargada y a continuación, a diferentes distancias, posicionó otra esfera también cargada. Luego midió la fuerza entre ellas observando el ángulo que giraba la barra.
Dichas mediciones permitieron determinar que:


 y
y 










En términos matemáticos, la magnitud de la fuerza que cada una de las dos cargas puntuales
de la fuerza que cada una de las dos cargas puntuales  y
y  ejerce sobre la otra separadas por una distancia
ejerce sobre la otra separadas por una distancia  se expresa como:
se expresa como:
 y
y  separadas una distancia
separadas una distancia  en el vacío, se atraen o repelen entre sí con una fuerza cuya magnitud está dada por:
en el vacío, se atraen o repelen entre sí con una fuerza cuya magnitud está dada por:
 es un vector unitario, siendo su dirección desde la cargas que produce la fuerza hacia la carga que la experimenta.
es un vector unitario, siendo su dirección desde la cargas que produce la fuerza hacia la carga que la experimenta.
Al aplicar esta fórmula en un ejercicio, se debe colocar el signo de las cargas q1 o q2, según sean éstas positivas o negativas.
El exponente (de la distancia: d) de la Ley de Coulomb es, hasta donde se sabe hoy en día, exactamente 2. Experimentalmente se sabe que, si el exponente fuera de la forma , entonces
, entonces  .
.
Obsérvese que esto satisface la tercera de la ley de Newton debido a que implica que fuerzas de igual magnitud actúan sobre y
y  .
La ley de Coulomb es una ecuación vectorial e incluye el hecho de que
la fuerza actúa a lo largo de la línea de unión entre las cargas.
.
La ley de Coulomb es una ecuación vectorial e incluye el hecho de que
la fuerza actúa a lo largo de la línea de unión entre las cargas.
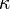 es la Constante de Coulomb y su valor para unidades SI es
es la Constante de Coulomb y su valor para unidades SI es  Nm²/C².
Nm²/C².
A su vez la constante donde
donde  es la permitividad relativa,
es la permitividad relativa,  , y
, y  F/m es la permitividad del medio en el vacío.
F/m es la permitividad del medio en el vacío.
Cuando el medio que rodea a las cargas no es el vacío hay que tener en cuenta la constante dieléctrica y la permitividad del material.
La ecuación de la ley de Coulomb queda finalmente expresada de la siguiente manera:
La constante, si las unidades de las cargas se encuentran en Coulomb es la siguiente  y su resultado será en sistema MKS (
y su resultado será en sistema MKS ( ). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma
). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma  y su resultado estará en las unidades CGS (
y su resultado estará en las unidades CGS ( ).
).
 se le asigna una función escalar o potencial de Coulomb
se le asigna una función escalar o potencial de Coulomb  tal que la fuerza dada por la ley de Coulomb sea expresable como:
tal que la fuerza dada por la ley de Coulomb sea expresable como:
 , es el vector de posición de la carga eléctrica
, es el vector de posición de la carga eléctrica  cuyo campo pretende caracterizarse por medio del potencia
cuyo campo pretende caracterizarse por medio del potencia
 . En el equilibrio:
. En el equilibrio:
 la separación de equilibrio entre las esferas cargadas, la fuerza
la separación de equilibrio entre las esferas cargadas, la fuerza  de repulsión entre ellas, vale, de acuerdo con la ley de Coulomb
de repulsión entre ellas, vale, de acuerdo con la ley de Coulomb  y, por lo tanto, se cumple la siguiente igualdad:
y, por lo tanto, se cumple la siguiente igualdad:
 y la fuerza de repulsíón entre las mismas estará dada por:
y la fuerza de repulsíón entre las mismas estará dada por:
 . Y de modo similar se obtiene:
. Y de modo similar se obtiene:
 y
y  y las separaciones entre las cargas
y las separaciones entre las cargas  y
y  es posible verificar que la igualdad se cumple dentro del error
experimental. En la práctica, los ángulos pueden resultar difíciles de
medir, así que si la longitud de los hilos que sostienen las esferas son
lo suficientemente largos, los ángulos resultarán lo bastante pequeños
como para hacer la siguiente aproximación:
es posible verificar que la igualdad se cumple dentro del error
experimental. En la práctica, los ángulos pueden resultar difíciles de
medir, así que si la longitud de los hilos que sostienen las esferas son
lo suficientemente largos, los ángulos resultarán lo bastante pequeños
como para hacer la siguiente aproximación:
La ley de la gravitación universal establece que la fuerza de atracción entre dos masas es directamente proporcional al producto de las mismas e inversamente proporcional al cuadrado de la distancia que las separa. Expresándolo matemáticamente:
 y
y  respectivamente y sus masas son
respectivamente y sus masas son  y
y  . Sustituyendo los datos:
. Sustituyendo los datos:
Si fuera posible concentrar la mencionada carga en dos puntos con una separación de 1 metro, la fuerza de interacción sería:
PARA MAYOR INFORMACIÓN .:
En la barra de la balanza, Coulomb colocó una pequeña esfera cargada y a continuación, a diferentes distancias, posicionó otra esfera también cargada. Luego midió la fuerza entre ellas observando el ángulo que giraba la barra.
Dichas mediciones permitieron determinar que:
- La fuerza de interacción entre dos cargas
 y
y  duplica su magnitud si alguna de las cargas dobla su valor, la triplica
si alguna de las cargas aumenta su valor en un factor de tres, y así
sucesivamente. Concluyó entonces que el valor de la fuerza era
proporcional al producto de las cargas:
duplica su magnitud si alguna de las cargas dobla su valor, la triplica
si alguna de las cargas aumenta su valor en un factor de tres, y así
sucesivamente. Concluyó entonces que el valor de la fuerza era
proporcional al producto de las cargas:


 y
y 




- Si la distancia entre las cargas es
 ,
al duplicarla, la fuerza de interacción disminuye en un factor de 4
(2²); al triplicarla, disminuye en un factor de 9 (3²) y al cuadriplicar
,
al duplicarla, la fuerza de interacción disminuye en un factor de 4
(2²); al triplicarla, disminuye en un factor de 9 (3²) y al cuadriplicar
 ,
la fuerza entre cargas disminuye en un factor de 16 (4²). En
consecuencia, la fuerza de interacción entre dos cargas puntuales, es
inversamente proporcional al cuadrado de la distancia:
,
la fuerza entre cargas disminuye en un factor de 16 (4²). En
consecuencia, la fuerza de interacción entre dos cargas puntuales, es
inversamente proporcional al cuadrado de la distancia:






Enunciado de la ley:
La ley de Coulomb es válida sólo en condiciones estacionarias, es decir, cuando no hay movimiento de las cargas o, como aproximación cuando el movimiento se realiza a velocidades bajas y en trayectorias rectilíneas uniformes. Es por ello que es llamada fuerza electrostática.En términos matemáticos, la magnitud
 de la fuerza que cada una de las dos cargas puntuales
de la fuerza que cada una de las dos cargas puntuales  y
y  ejerce sobre la otra separadas por una distancia
ejerce sobre la otra separadas por una distancia  se expresa como:
se expresa como:Dadas dos cargas puntuales
 y
y  separadas una distancia
separadas una distancia  en el vacío, se atraen o repelen entre sí con una fuerza cuya magnitud está dada por:
en el vacío, se atraen o repelen entre sí con una fuerza cuya magnitud está dada por:La Ley de Coulomb se expresa mejor con magnitudes vectoriales:
donde
 es un vector unitario, siendo su dirección desde la cargas que produce la fuerza hacia la carga que la experimenta.
es un vector unitario, siendo su dirección desde la cargas que produce la fuerza hacia la carga que la experimenta.Al aplicar esta fórmula en un ejercicio, se debe colocar el signo de las cargas q1 o q2, según sean éstas positivas o negativas.
El exponente (de la distancia: d) de la Ley de Coulomb es, hasta donde se sabe hoy en día, exactamente 2. Experimentalmente se sabe que, si el exponente fuera de la forma
 , entonces
, entonces  .
.Obsérvese que esto satisface la tercera de la ley de Newton debido a que implica que fuerzas de igual magnitud actúan sobre
 y
y  .
La ley de Coulomb es una ecuación vectorial e incluye el hecho de que
la fuerza actúa a lo largo de la línea de unión entre las cargas.
.
La ley de Coulomb es una ecuación vectorial e incluye el hecho de que
la fuerza actúa a lo largo de la línea de unión entre las cargas.Constante de Coulomb.
La constante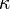 es la Constante de Coulomb y su valor para unidades SI es
es la Constante de Coulomb y su valor para unidades SI es  Nm²/C².
Nm²/C².A su vez la constante
 donde
donde  es la permitividad relativa,
es la permitividad relativa,  , y
, y  F/m es la permitividad del medio en el vacío.
F/m es la permitividad del medio en el vacío.Cuando el medio que rodea a las cargas no es el vacío hay que tener en cuenta la constante dieléctrica y la permitividad del material.
La ecuación de la ley de Coulomb queda finalmente expresada de la siguiente manera:
 |
|---|
 y su resultado será en sistema MKS (
y su resultado será en sistema MKS ( ). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma
). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma  y su resultado estará en las unidades CGS (
y su resultado estará en las unidades CGS ( ).
).Potencial de Coulomb
La ley de Coulomb establece que la presencia de una carga puntual general induce en todo el espacio la aparición de un campo de fuerzas que decae según la ley de la inversa del cuadrado. Para modelizar el campo debido a varias cargas eléctricas puntuales estáticas puede usarse el principio de superposición dada la aditividad de las fuerzas sobre una partícula. Sin embargo, matemáticamente el manejo de expresiones vectoriales de ese tipo puede llegar a ser complicado, por lo que frecuentemente resulta más sencillo definir un potencial eléctrico. Para ello a una carga puntual se le asigna una función escalar o potencial de Coulomb
se le asigna una función escalar o potencial de Coulomb  tal que la fuerza dada por la ley de Coulomb sea expresable como:
tal que la fuerza dada por la ley de Coulomb sea expresable como:De la ley de Coumlomb se deduce que la función escalar que satisface la anterior ecuación es:
Donde:
 , es el vector posición genérico de un punto donde se pretende definir el potencial de Coulomb y
, es el vector posición genérico de un punto donde se pretende definir el potencial de Coulomb y
 , es el vector de posición de la carga eléctrica
, es el vector de posición de la carga eléctrica  cuyo campo pretende caracterizarse por medio del potencia
cuyo campo pretende caracterizarse por medio del potenciaLimitaciones de la Ley de Coulomb
- La expresión matemática solo es aplicable a cargas puntuales estacionarias, y para casos estáticos más complicados de carga necesita ser generalizada mediante el potencial eléctrico.
- Cuando las cargas eléctricas están en movimiento es necesario reemplazar incluso el potencial de Coulomb por el potencial vector de Liénard-Wiechert, especialmente si las velocidades de las partículas son grandes comparadas con la velocidad de la luz.
- Para distancias pequeñas (del orden del tamaño de los átomos), la fuerza electrostática se ve superada por otras, como la nuclear fuerte, o la nuclear débil.
Verificación experimental de la Ley de Coulomb
Es posible verificar la ley de Coulomb mediante un experimento sencillo. Considérense dos pequeñas esferas de masa "m" cargadas con cargas iguales, del mismo signo, y que cuelgan de dos hilos de longitud l, tal como se indica en la figura adjunta. Sobre cada esfera actúan tres fuerzas: el peso mg, la tensión de la cuerda T y la fuerza de repulsión eléctrica entre las bolitas . En el equilibrio:
. En el equilibrio:(1)y también:
(2)Dividiendo () entre () miembro a miembro, se obtiene:
Siendo
 la separación de equilibrio entre las esferas cargadas, la fuerza
la separación de equilibrio entre las esferas cargadas, la fuerza  de repulsión entre ellas, vale, de acuerdo con la ley de Coulomb
de repulsión entre ellas, vale, de acuerdo con la ley de Coulomb  y, por lo tanto, se cumple la siguiente igualdad:
y, por lo tanto, se cumple la siguiente igualdad:(3)Al descargar una de las esferas y ponerla, a continuación, en contacto con la esfera cargada, cada una de ellas adquiere una carga q/2, en el equilibrio su separación será
 y la fuerza de repulsíón entre las mismas estará dada por:
y la fuerza de repulsíón entre las mismas estará dada por:Por estar en equilibrio, tal como se dedujo más arriba:
 . Y de modo similar se obtiene:
. Y de modo similar se obtiene:(4)Dividiendo () entre (), miembro a miembro, se llega a la siguiente igualdad:
(5)Midiendo los ángulos
 y
y  y las separaciones entre las cargas
y las separaciones entre las cargas  y
y  es posible verificar que la igualdad se cumple dentro del error
experimental. En la práctica, los ángulos pueden resultar difíciles de
medir, así que si la longitud de los hilos que sostienen las esferas son
lo suficientemente largos, los ángulos resultarán lo bastante pequeños
como para hacer la siguiente aproximación:
es posible verificar que la igualdad se cumple dentro del error
experimental. En la práctica, los ángulos pueden resultar difíciles de
medir, así que si la longitud de los hilos que sostienen las esferas son
lo suficientemente largos, los ángulos resultarán lo bastante pequeños
como para hacer la siguiente aproximación:Con esta aproximación, la relación () se transforma en otra mucho más simple:
De esta forma, la verificación se reduce a medir la separación entre cargas y comprobar que su cociente se aproxima al valor indicado.
Comparación entre la Ley de Coulomb y la Ley de la Gravitación Universal
Esta comparación es relevante ya que ambas leyes dictan el comportamiento de dos de las fuerzas fundamentales de la naturaleza mediante expresiones matemáticas cuya similitud es notoria.La ley de la gravitación universal establece que la fuerza de atracción entre dos masas es directamente proporcional al producto de las mismas e inversamente proporcional al cuadrado de la distancia que las separa. Expresándolo matemáticamente:
Siendo:
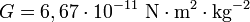 la constante de gravitación universal,
la constante de gravitación universal, las masas de los cuerpos en cuestión y
las masas de los cuerpos en cuestión y la distancia entre los centros de las masas.
la distancia entre los centros de las masas.
 y
y  respectivamente y sus masas son
respectivamente y sus masas son  y
y  . Sustituyendo los datos:
. Sustituyendo los datos:Al comparar resultados se observa que la fuerza eléctrica es de unos 39 órdenes de magnitud superior a la fuerza gravitacional. Lo que esto representa puede ser ilustrado mediante un ejemplo muy llamativo. 1 C equivale a la carga que pasa en 1 s por cualquier punto de un conductor por el que circula una corriente de intensidad 1 A constante. En viviendas con tensiones de 220 Vrms, esto equivale a un segundo de una bombilla de 220 W (120 W para las instalaciones domésticas de 120 Vrms).
.
Si fuera posible concentrar la mencionada carga en dos puntos con una separación de 1 metro, la fuerza de interacción sería:
o sea, ¡916 millones de kilopondios, o el peso de una masa de casi un millón de toneladas (un teragramo)!. Si tales cargas se pudieran concentrar de la forma indicada más arriba, se alejarían bajo la influencia de esta enorme fuerza. Si de esta hipotética disposición de cargas resultan fuerzas tan enormes, ¿por qué no se observan despliegues dramáticos debidos a las fuerzas eléctricas? La respuesta general es que en un punto dado de cualquier conductor nunca hay demasiado alejamiento de la neutralidad eléctrica. La naturaleza nunca acumula un Coulomb de carga en un punto.
PARA MAYOR INFORMACIÓN .:













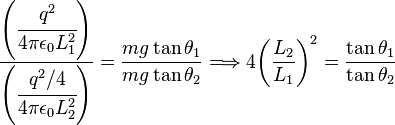
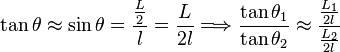
![\frac{L_1}{L_2}\approx 4 {\left ( \frac {L_2}{L_1} \right ) }^2\Longrightarrow \frac{L_1}{L_2}\approx\sqrt[3]{4} \,\!](http://upload.wikimedia.org/wikipedia/es/math/7/c/e/7cef359a7cd4a5f6a3be9d150a4a14e0.png)



No hay comentarios:
Publicar un comentario